| Definitions | True,  T, hd(l), i< T, hd(l), i< j, i j, i  j, P j, P  Q, Dec(P), Q, Dec(P),  b, b,   b, b,  , Unit, {T}, SQType(T), S , Unit, {T}, SQType(T), S 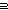 T, i= T, i= j, if b j, if b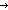 t else f fi, P t else f fi, P   Q, P Q, P   Q, l[i], ||as||, i Q, l[i], ||as||, i  j < k, S j < k, S  T, Prop, T, Prop,   x. t(x), sum(f(x) | x < k), x. t(x), sum(f(x) | x < k),  , t , t  T, T,  x:A. B(x), P x:A. B(x), P   Q, i Q, i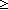 j, {i..j j, {i..j }, A & B, P & Q, }, A & B, P & Q,  x:A. B(x), False, x:A. B(x), False,  A, A A, A B, i>j B, i>j |